Understanding the Structure of Neural Networks
To understand how neural networks function, it is helpful to know the different parts of a network. Suppose we have the following network:
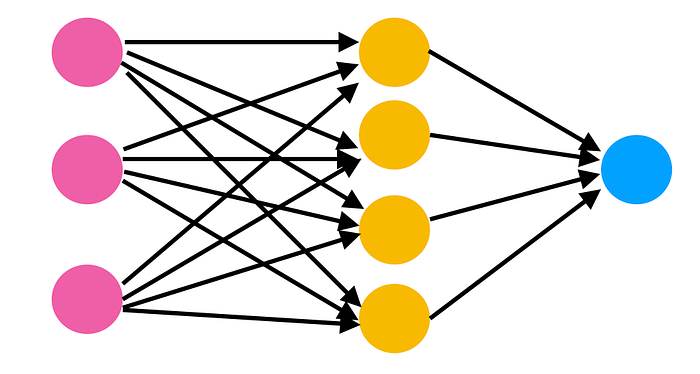
Now lets take a look at the basic steps of how a neural network works.
Basic steps:
- Our input neurons represent an input based on the information we are trying to classify
- Each number in the input neurons is given a weight at each synapse
- At each neuron in the next layer, we add the outputs of all synapses coming to that neuron along with a bias and apply an activation function (commonly a sigmoid function) to the weighted sum (this makes the number something between 0 and 1)
- The output of that function will be treated as the input for the next synapse layer
- Continue until you reach the output
Let’s look at a simple example:
Let’s say the input is the hours you slept and hours you studied; and you are trying to figure out what you will score on a test as a result. Some observations can be seen below:
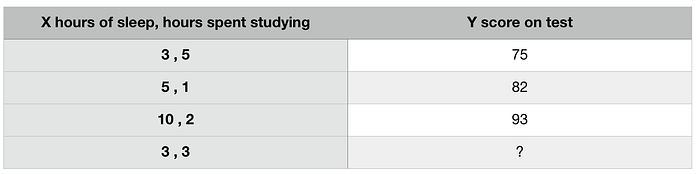
To be able to predict a score based on hours slept and hours spent studying, we need to train a model. Let’s first just look at how these inputs would be processed through a neural network. Let’s look at only the first input value (3,5). A representation of this process can be seen in the diagram below.
The input layer has two input neurons based on the hours of sleep and hours spent studying. We have a single output neuron for the score on the test. The number of layers and number of neurons in the hidden layer(s) is a bit arbitrary and we usually experiment to decide what works best for our particular model. It is important to note, however, that once this is chosen, it does not change throughout the model. It is considered one of our hyper parameters. The “learning” part of a neural net, and the parameters we train, are the various weights applied at each synapse.
Looking at our steps above, we can walk through our simple diagram example:
- Our input neurons represent an input based on the information we are trying to predict/classify
Here we put 3 in one input neuron and 5 in the other to represent hours of sleep and hours spent studying; these make up a single input observation.
2. Each number in the input neurons is given a weight at each synapse
The number of hours of sleep and the number of hours spent studying are weighted differently at each synapse
3. At each neuron in the next layer, we add the outputs of all synapses coming to that neuron and a bias and apply an activation function to the weighted sum (this makes the number something between 0 and 1)
The results of each synapse are added together to give us Zi(1) which is then passed into an activation function to give us a1i (this will be our activation number with a value between 0 and 1)
4. The output of that function will be treated as the input for the next synapse layer
The result of this function is treated as the new input and weighted
5. Continue until you reach the output
Since this example has only one hidden layer, the results of these synapses are added together and passed into a sigmoid activation function to give us our prediction for the first observation
The diagram above shows us the process for a single input. Doing this one at a time for each input pair is a bit cumbersome and would result in a very slow and inefficient code. Instead, we commonly process all inputs at one time using matrices.
To see how this works, we should first realize that we can represent the step from the input neurons to hidden layer neurons for all inputs as follows:

What we have in the red circle is the same thing we get in the diagram for Z1(1) Z2(1) Z3(1). As we can see, with matrix multiplication, we can quickly run through the process. All we need to do is write our results from the neurons in one layer as a column matrix and organize our weights as a row matrix. By matrix multiplication, we can get the weighted sum for each input observation. Building from this, the steps are quite similar as before but deal with all inputs at once.

This matrix form makes it so we can represent full transitions of activations from one layer to the next in an extremely tight and neat expression. This makes it much easier to code efficient neural networks.
The next step to understanding neural networks would be to to figure out how neural networks “learn”. Essentially, this is figuring out how to find the right weights for our model. This will be covered in the next blog.
Summary:
To understand how neural networks function, it is helpful to know the different parts of a network. Suppose we have the following network: Let’s say the input is the hours you slept and hours you…